揭秘补集定义与表示方法，轻松掌握数学核心概念！

补集，作为集合论中的一个基本概念，是理解集合间关系的重要工具。它为我们提供了一种描述“不属于某个集合”的元素集合的方法，从而在逻辑、数学、计算机科学等多个领域中得到广泛应用。本文将深入探讨补集的定义、表示方式及其重要性，帮助有兴趣了解这一概念的读者更好地掌握其精髓。

补集的定义

在集合论中，补集是一个相对的概念，它依赖于一个更广泛的集合，即全集（Universal Set）。全集是包含我们当前研究问题中所有可能元素的集合。给定一个集合A和它的全集U，A在U中的补集（Complement Set），通常记作∁U(A)或A'，是由U中所有不属于A的元素组成的集合。简单来说，补集就是全集U中去掉集合A后剩余的部分。

需要注意的是，补集的定义依赖于全集的选择。在不同的上下文中，全集可能不同，因此同一集合的补集也会有所不同。例如，在整数范围内，全集U可以是所有整数的集合Z；而在实数范围内，全集U则扩展为所有实数的集合R。

补集的表示

补集的表示方法通常有两种：符号表示和描述法表示。

符号表示

补集的符号表示直观且简洁，主要通过在集合符号前加上补集符号（如∁或'）来表示。例如，集合A在全集U中的补集可以表示为∁U(A)或A'。这种表示方法简洁明了，便于在公式和定理中直接使用。

描述法表示

除了符号表示外，补集还可以通过描述法来表示。描述法是通过描述集合中元素的特征来定义集合的一种方法。对于集合A在全集U中的补集A'，其描述法表示为{x | x ∈ U 且 x ∉ A}。这里，x表示全集U中的任意元素，x ∉ A表示x不属于集合A。通过这种方式，我们可以清晰地知道补集A'包含了哪些元素。

补集的类型

在集合论中，补集还可以进一步细分为相对补集和绝对补集。

相对补集

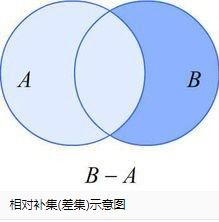
相对补集是指在一个集合内部，相对于另一个集合的补集。设A和B是两个集合，那么A在B中的相对补集定义为B中所有不属于A的元素组成的集合，记作B-A或A\B（在某些文献中，也使用A-B来表示，但这里为了与减法区分，我们使用B-A）。即B-A = {x | x ∈ B 且 x ∉ A}。相对补集描述了两个集合之间不包含对方元素的部分。

绝对补集

绝对补集（或简称补集）则是相对于全集而言的。如前所述，A在全集U中的补集即为A的绝对补集，记作∁U(A)或A'。绝对补集是补集概念中更为基础和核心的部分，它建立了集合与全集之间的一种重要关系。

补集的性质与运算

补集不仅具有明确的定义和表示方式，还具备一系列重要的性质和运算规律。

性质

1. 互补性：补集与原集合在全集中没有交集，即A ∩ A' = ∅（空集）。同时，补集与原集合的并集等于全集，即A ∪ A' = U。

2. 对称性：若A是U的子集，则A的补集A'也是U的子集，且A'的补集等于A，即(A')' = A。

3. 德摩根定律（或称反演律）：描述了两个集合的交集的补集与它们各自补集的并集之间的关系，以及两个集合的并集的补集与它们各自补集的交集之间的关系。具体地，有∁(A ∩ B) = ∁A ∪ ∁B和∁(A ∪ B) = ∁A ∩ ∁B。

运算

补集运算与其他集合运算（如交集、并集）之间存在紧密的联系。例如，在求解某些复杂集合表达式时，通过转化为补集运算往往能简化问题。此外，补集运算还满足一些基本的运算法则，如求补律（A ∪ ∁A = U，A ∩ ∁A = ∅）等。

应用领域

补集的概念和性质在多个领域中得到广泛应用。

逻辑运算

在逻辑学中，补集对应于命题的否定。如果A表示一个命题为真，那么A'（或¬A）则表示该命题