揭开黎曼假设的神秘面纱

黎曼假设，这一数学领域的重大猜想，自19世纪德国数学家波恩哈德·黎曼提出以来，便在数学界引起了广泛的关注与研究。它不仅深刻影响了数论的发展，还与众多其他数学分支及物理学理论有着千丝万缕的联系。本文旨在以简洁明了的语言，全面介绍黎曼假设的基本概念、历史背景、证明尝试、现状及其重要意义。

一、黎曼假设的基本概念

黎曼假设是关于黎曼ζ函数（Riemann Zeta Function）的零点分布的猜想。ζ函数，记作ζ(s)，是一个在复数域上定义的函数，其表达式为ζ(s)=Σ(n=1至∞) (1/n^s)，其中s为复数，n为正整数。这个函数在数论中占据核心地位，因为它与素数的分布规律紧密相关。

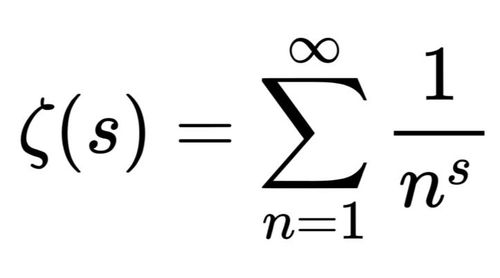
黎曼ζ函数的零点，即满足ζ(s)=0的s值，分为两类：平凡零点和非平凡零点。平凡零点是指s=-2, -4, -6,...等负偶数的情况，这些零点的分布规律简单且已知。而非平凡零点的性质则复杂得多，它们的位置至今尚未完全确定。

黎曼假设断言，所有非平凡零点的实部均严格等于1/2。换句话说，如果我们将复平面上的点表示为(Re(s), Im(s))，其中Re(s)和Im(s)分别表示复数s的实部和虚部，那么黎曼假设就是说，所有非平凡零点都位于直线Re(s)=1/2上，这条直线也被称为临界线（critical line）。

二、黎曼假设的历史背景

黎曼假设的提出源于黎曼对素数分布规律的深入探索。素数，即只能被1和自身整除的自然数，是数论中最基本也是最重要的研究对象之一。黎曼观察到，素数的频率与精心构造的黎曼ζ函数的性态紧密相关。因此，他试图通过研究ζ函数的性质来揭示素数的分布规律。

1859年，黎曼在其论文《论小于给定数值的素数个数》中正式提出了这一猜想。他利用复分析的方法，将素数计数问题转化为对黎曼ζ函数零点的研究。这一开创性的工作不仅为数论开辟了新的研究方向，也为后来的数学家们提供了宝贵的思路和方法。

三、黎曼假设的证明尝试与现状

自黎曼提出假设以来，无数数学家为之付出了巨大的努力。然而，尽管取得了许多重要的进展和成果，但黎曼假设至今仍未得到证明或否定。

证明黎曼假设的难度极大，它涉及到了数学中许多最复杂和深奥的概念和技巧。数学家们尝试了各种方法，包括解析数论、代数几何、复分析等多个领域的知识，但始终未能找到确凿的证据来证明或反驳这一猜想。

尽管如此，数学家们仍在不断地探索和研究。他们利用计算机进行大规模的数值计算，试图找到反例或支持黎曼假设的证据。同时，他们也在努力寻找新的数学工具和方法，以期能够突破这一难题。

值得注意的是，虽然黎曼假设尚未得到证明，但它已经在数学界产生了深远的影响。许多重要的数学命题和定理都以黎曼假设的成立为前提。一旦黎曼假设得到证明或否定，这些数学命题和定理也将得到新的认识和解读。

四、黎曼假设的重要意义

黎曼假设不仅是数学领域中的一个重大猜想，它还与众多其他数学问题存在着紧密的联系。例如，它与费马大定理、庞加莱猜想等著名数学难题都有着千丝万缕的联系。一旦黎曼假设得到证明或否定，这些数学难题也将受到新的认识和解读。

此外，黎曼假设还与数学中的许多基本概念和理论密切相关，如复变函数论、调和分析等。对黎曼假设的研究不仅有助于解决这一未解之谜本身，还有助于推动数学学科整体的发展。

更重要的是，黎曼假设在物理学领域也有着潜在的应用价值。它与广义相对论和量子力学等物理学理论有着深刻的联系。一些物理学家甚至认为，黎曼假设的解决将有助于揭示宇宙的基本结构和运动规律。

五、结语

黎曼假设作为数学领域中最重要且尚未解决的问题之一，其解决将对数学及相关学科的发展产生深远的影响。尽管目前尚未得到证明或否定，但数学家们仍在不断地努力探索和研究这一未解之谜。他们相信，在不久的将来，黎曼假设的真相将得以揭示，为数学领域带来新的突破和进展。

黎曼假设的研究不仅是对数学真理的追求，更是对人类智慧和创造力的挑战。它激发了数学家们不断探索未知领域的勇气和决心，也为我们揭示了数学世界的无限魅力和广阔前景。在未来的日子里，让我们共同期待黎曼假设的解决，见证数学领域的辉煌成就。