探索二次函数：图像之美与性质之谜

二次函数是数学中的基本概念之一，在代数、几何等多个领域中都有广泛应用。理解二次函数的图像和性质，对解决相关问题具有重要意义。本文将从定义、图像特征、基本性质、顶点坐标公式及求解、对称轴和开口方向、与坐标轴的交点、实际应用等多个维度，详细探讨二次函数的图像和性质。

定义

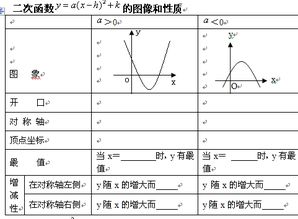
二次函数的一般形式为f(x) = ax² + bx + c，其中a、b、c为实数，且a ≠ 0。这里的a决定了函数的开口方向和开口大小，b和c则影响图像的位置和形状。当a > 0时，图像开口向上；当a < 0时，图像开口向下。

图像特征

二次函数的图像是一条抛物线。抛物线的形状和位置由系数a、b、c共同决定。具体来说，抛物线的开口方向由a决定，开口大小由|a|决定，|a|越大，开口越小；|a|越小，开口越大。b和c则决定抛物线的左右平移和上下平移。

基本性质

1. 最值性：由于抛物线关于其对称轴对称，因此它有一个最高点或最低点，称为顶点。当a > 0时，抛物线有最低点，即函数有最小值；当a < 0时，抛物线有最高点，即函数有最大值。

2. 单调性：抛物线在其对称轴两侧的单调性相反。当a > 0时，抛物线在对称轴左侧是单调递减的，在对称轴右侧是单调递增的；当a < 0时，抛物线在对称轴左侧是单调递增的，在对称轴右侧是单调递减的。

3. 奇偶性：二次函数f(x) = ax² + bx + c既不是奇函数也不是偶函数（除非b = 0，此时函数为偶函数）。

4. 有界性：抛物线在y轴方向上有界（即有最大值或最小值），在x轴方向上无界。

顶点坐标公式及求解

顶点坐标是二次函数图像上的一个重要点，也是求解函数最值的关键。对于一般形式的二次函数f(x) = ax² + bx + c，其顶点坐标为(-b/(2a), c - b²/(4a))。这个公式可以通过配方法得到：

f(x) = ax² + bx + c

= a(x² + (b/a)x) + c

= a(x² + (b/a)x + (b/2a)² - (b/2a)²) + c

= a(x + b/(2a))² - b²/(4a) + c

= a(x - (-b/(2a)))² + (c - b²/(4a))

从上式可以看出，当x = -b/(2a)时，函数取得最值y = c - b²/(4a)，即顶点坐标为(-b/(2a), c - b²/(4a))。

对称轴和开口方向

对称轴是二次函数图像的一条重要直线，它经过抛物线的顶点，并将抛物线分为左右对称的两部分。对于一般形式的二次函数f(x) = ax² + bx + c，其对称轴方程为x = -b/(2a)。

开口方向由系数a决定。当a > 0时，抛物线开口向上；当a < 0时，抛物线开口向下。开口大小由|a|决定，|a|越大，开口越小；|a|越小，开口越大。

与坐标轴的交点

1. 与x轴的交点：即求解方程ax² + bx + c = 0的根。根据一元二次方程的求根公式，其解为x = [-b ± √(b²-4ac)]/(2a)。当Δ = b²-4ac > 0时，方程有两个不相等的实根；当Δ = 0时，方程有两个相等的实根（即一个二重根）；当Δ < 0时，方程无实根（即抛物线不与x轴相交）。

2. 与y轴的交点：即求解函数在x = 0时的值。将x = 0代入函数f(x) = ax² + bx + c中，得到y = c。因此，抛物线与y轴的交点坐标为(0, c)。

实际应用

二次函数在生活和科学研究中有着广泛的应用。以下列举几个常见的应用场景：

1. 物理学中的抛物线运动：物体在只受重力作用下的运动轨迹是抛物线。通过求解二次函数方程，可以得到物体的运动距离、时间和高度等信息。

2. 经济学中的