arcsinx与sinx分之一有何关系？

在数学领域中，对于反三角函数与三角函数之间的关系，常常引起初学者的疑惑，尤其是关于arcsinx是否等于sinx分之一的问题。为了深入理解这一问题，我们可以从多个维度进行探讨，包括反三角函数与三角函数的基本概念、arcsinx与sinx的具体关系、以及通过实例进一步说明。

一、反三角函数与三角函数的基本概念

在数学中，反三角函数（antitrigonometric functions），也称为弓形函数（arcus functions）、反向函数（reverse function）或环形函数（cyclometric functions），是三角函数的反函数。三角函数，如正弦（sin）、余弦（cos）和正切（tan），描述了直角三角形中边长与角度的关系。由于三角函数具有周期性，因此其反函数需要限制在特定的域内，以保证每个值都有唯一的反函数。

二、arcsinx与sinx的关系

1. arcsinx的定义

arcsinx是正弦函数sinx的反函数。这意味着，如果sinx=y，那么arcsiny=x。由于sinx的取值范围是[-1, 1]，因此arcsinx的取值范围是(-π/2, π/2)。arcsinx用于表示一个正弦值为x的角，该角位于-π/2到π/2之间。

2. sinx与arcsinx的计算关系

已知sinx的值，要求arcsinx的值，可以按照以下步骤进行：

确定sinx的取值范围：如果sinx的值超出[-1, 1]，则arcsinx不存在。

确定arcsinx所在的象限：根据sinx的正负号和绝对值，可以判断arcsinx落在哪个象限。

计算arcsinx的值：使用计算器或查表求出arcsinx的值。

例如，如果sinx=0.5，则：

sinx=0.5在[-1, 1]范围内。

sinx>0，因此arcsinx在第一象限。

使用计算器计算得arcsinx≈0.5236弧度。

3. arcsinx不等于1/sinx

重要的是要明确指出，arcsinx并不等于1/sinx。这是一个常见的误解。arcsinx是sinx的反函数，表示的是一个角度，而1/sinx是sinx的倒数，表示的是一个比值。两者在数学上是完全不同的概念。

三、通过实例进一步说明

为了更深入地理解arcsinx与sinx的关系，我们可以通过一些实例来进一步说明。

1. 已知sinx求arcsinx

假设sinx=√3/2，我们需要求出arcsinx的值。

首先，确认sinx的取值范围。√3/2在[-1, 1]范围内，因此arcsinx存在。

其次，判断arcsinx所在的象限。由于sinx>0，且其值大于1/2（sinπ/6=1/2），因此arcsinx在第一象限，并且大于π/6。

最后，使用计算器或查表求出arcsinx的值。计算得arcsin(√3/2)=π/3。

2. 已知arcsinx求sinx

假设arcsinx=π/6，我们需要求出sinx的值。

由于arcsinx=π/6，根据反正弦函数的定义，我们可以直接得出sin(arcsinx)=sin(π/6)=1/2。

因此，sinx=1/2。

四、arcsinx的性质与图像

1. arcsinx的性质

奇函数性质：arcsin(-x)=-arcsinx。

单调性：在[-1, 1]区间内，arcsinx是单调递增的。

值域：arcsinx的值域是(-π/2, π/2)。

2. arcsinx的图像

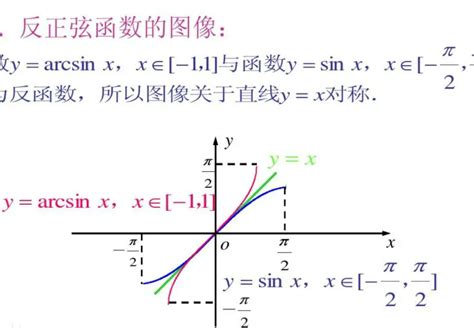
正弦函数的图像和反正弦函数的图像关于一三象限角平分线对称。这是因为，如果一个点是正弦函数图像上的点，那么它关于一三象限角平分线的对称点就是反正弦函数图像上的点。

五、arcsinx与sinx在实际问题中的应用

arcsinx与sinx在物理学、工程学以及日常生活中都有广泛的应用。例如，在物理学中，研究简谐振动时，正弦函数和反正弦函数经常用于描述位移、速度和加速度随时间的变化。在工程学中，反三角函数用于计算角度、长度和面积等几何量。在日常生活中，例如在音乐中，正弦波和反正弦函数用于描述声音的波形和频率。

六、总结

综上所述，arcsinx并不等于sinx分之一。arcsinx是正弦函数sinx的反函数，表示一个正弦值为x的角，而1/sinx是sinx的倒数。两者在数学上是完全不同的概念。通过深入理解反三角函数与三角函数的基本概念、arcsinx与sinx的具体关系以及