在微积分学中,二重积分是一个极其重要的概念,它不仅是单变量函数积分理论在多维空间上的自然推广,也是解决诸多物理、工程及经济问题中面积、体积、质量分布等计算的关键工具。要深入理解并掌握二重积分$\int\int f(x,y) \,dxdy$的计算方法,我们可以从定义、计算步骤、技巧、应用以及几何意义等多个维度进行探讨。
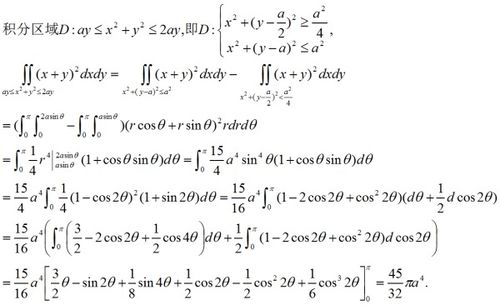
二重积分,顾名思义,是对两个变量在指定区域内进行积分的过程。设函数$f(x,y)$在闭区域$D$上有定义,且对$D$的任意子区域$\Delta \sigma$,当$\Delta \sigma$的面积$\Delta S \to 0$时,和式极限

$$\lim_{{\Delta S \to 0}} \sum_{i=1}^{n} f(\xi_i,\eta_i) \Delta S_i$$

如果存在,则称此极限为函数$f(x,y)$在区域$D$上的二重积分,记作
$$\int\int_{D} f(x,y) \,dxdy$$
其中,$\xi_i, \eta_i$是$\Delta \sigma_i$内任取的一点,$\Delta S_i$是$\Delta \sigma_i$的面积。
首先,明确积分区域$D$的边界,这通常通过给定的一组不等式或曲线方程来确定。
直角坐标系:若区域$D$容易用$x,y$的不等式表示,常选择先对$y$积分再对$x$积分(或相反),即先确定$x$的取值范围,再对每一个$x$值确定$y$的取值范围。
极坐标系:对于某些具有圆形或旋转对称性的区域,使用极坐标$(r,\theta)$进行积分更为方便。转换关系为$x = r\cos\theta, y = r\sin\theta$,同时面积元素变为$dS = r \,dr\,d\theta$。
根据选择的积分次序,先对内层变量进行积分,得到关于外层变量的函数,再对外层变量进行积分。
将内层积分的结果代入外层积分的表达式中,计算最终的定积分值。
1. 对称性简化:如果积分区域或被积函数具有某种对称性,可以利用这些性质简化计算。例如,奇函数在对称区间上的积分为零。
2. 换元法:对于复杂的被积函数,尝试通过换元简化表达式。在二重积分中,换元后需注意积分区域的相应变化。
3. 分割区域:当积分区域复杂或难以直接积分时,可以尝试将区域分割为几个易于处理的子区域,分别计算后再求和。
4. 利用几何意义:二重积分在几何上表示平面区域$D$上曲顶柱体的体积,或被积函数在$D$上的“质量”分布。这一性质有助于直观理解二重积分的计算过程和结果。
1. 面积计算:当被积函数为1时,二重积分即为所给区域的面积。
2. 体积计算:在三维空间中,二重积分可用于计算由曲面$z = f(x,y)$、平面$z = c$($c$为常数)及平面区域$D$围成的立体体积。
3. 物理问题:在物理学中,二重积分广泛应用于计算压力分布下的总压力、质量分布下的总质量、热流量等。
4. 经济学应用:在经济学中,二重积分可用于估算资源分配问题中的总成本、总收益等。
二重积分的几何意义是:在平面区域$D$上,以$f(x,y)$为顶面,$D$为底面的曲顶柱体的体积。这一解释不仅使二重积分的概念更加直观,也为其在各个领域的应用提供了物理背景。
综上所述,二重积分是微积分学中的一个重要工具,其计算涉及定义理解、积分次序选择、坐标变换、技巧应用等多个方面。通过掌握这些基本概念和计算方法,我们能够有效地解决众多实际问题中的积分问题,进一步拓展微积分的应用领域。
72.76M周公解梦大全2345原版
60.38M活力充电
66M哮天犬容器科技
53.83M小鸟电视
29.81M病娇模拟器旧版
54.92M万能遥控器大师极速版
9.66M病娇模拟器同人1.5.6版本
69.39M速影TV电视版
21.08M旅行翻译官
85.45M南充一卡通
本站所有软件来自互联网,版权归原著所有。如有侵权,敬请来信告知 ,我们将及时删除。 琼ICP备2024021917号-10