掌握三角函数公式，轻松解题无压力！

三角函数是数学中的基本概念之一，广泛应用于几何、物理、工程等领域。了解和掌握三角函数公式是学习和应用这些领域知识的基础。以下是一篇关于三角函数公式的文章，旨在通过详细阐述和列举，帮助读者更好地理解和记忆这些重要公式。

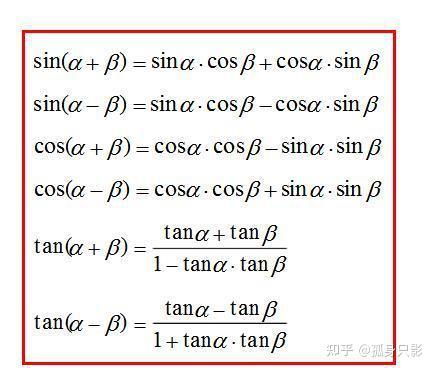
三角函数公式主要包括正弦、余弦、正切、余切、正割和余割等基本函数。它们之间的关系以及在不同象限内的符号变化是学习和应用这些公式时需要特别注意的地方。

正弦函数sin(θ)的定义为对边比斜边，在直角三角形中，对边是与角θ相对的边，斜边是三角形的最长边。正弦函数的公式包括基本公式sin(θ) = a/c（a为对边，c为斜边），以及诱导公式sin(α ± β) = sinαcosβ ± cosαsinβ。此外，正弦函数还有倍角公式sin2α = 2sinαcosα和半角公式sin(α/2) = ±√[(1 - cosα)/2]。这些公式在解决三角函数问题时非常有用，可以简化计算过程。

余弦函数cos(θ)的定义为邻边比斜边，在直角三角形中，邻边是与角θ相邻的边。余弦函数的公式同样包括基本公式cos(θ) = b/c（b为邻边，c为斜边），以及诱导公式cos(α ± β) = cosαcosβ ∓ sinαsinβ。余弦函数也有倍角公式cos2α = cos²α - sin²α和半角公式cos(α/2) = ±√[(1 + cosα)/2]。这些公式在求解与余弦相关的三角函数问题时同样具有重要意义。

正切函数tan(θ)的定义为对边比邻边，即tan(θ) = sin(θ)/cos(θ)。正切函数的公式包括基本公式tan(θ) = a/b（a为对边，b为邻边），以及诱导公式tan(α ± β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)。正切函数还有倍角公式tan2α = (2tanα)/(1 - tan²α)和半角公式tan(α/2) = ±√[(1 - cosα)/(1 + cosα)] = (1 - cosα)/sinα = sinα/(1 + cosα)。这些公式在解决正切相关的三角函数问题时非常有用，可以大大提高解题效率。

余切函数cot(θ)是正切函数的倒数，即cot(θ) = 1/tan(θ) = cos(θ)/sin(θ)。余切函数的公式包括基本公式cot(θ) = b/a（b为邻边，a为对边），以及诱导公式cot(α ± β) = (cotαcotβ - 1) ± cotα + cotβ/(cotα + cotβ) ∓ 1。余切函数还有倍角公式cot2α = (cot²α - 1)/(2cotα)和半角公式cot(α/2) = ±√[(1 + cosα)/(1 - cosα)] = (1 + cosα)/sinα = sinα/(cosα - 1)。

正割函数sec(θ)是余弦函数的倒数，即sec(θ) = 1/cos(θ)。正割函数的公式包括基本公式sec(θ) = c/b（c为斜边，b为邻边），以及诱导公式sec(α ± β) = (secαsecβ)/(1 ± tanαtanβ)。正割函数还有倍角公式sec2α = 1/(cos²α - sin²α)和半角公式sec(α/2) = ±√[2/(1 + cosα)]。

余割函数csc(θ)是正弦函数的倒数，即csc(θ) = 1/sin(θ)。余割函数的公式包括基本公式csc(θ) = c/a（c为斜边，a为对边），以及诱导公式csc(α ± β) = (cscαcscβ)/(1 ∓ cotαcotβ)。余割函数还有倍角公式csc2α = 1/(sin²α)和半角公式csc(α/2) = ±√[2/(1 - cosα)]。

除了上述基本三角函数公式外，还有一些重要的和差化积公式和积化和差公式。和差化积公式包括sinθ + sinφ = 2sin[(θ + φ)/2]cos[(θ - φ)/2]、sinθ - sinφ = 2cos[(θ + φ)/2]sin[(θ - φ)/2]、cosθ + cosφ = 2cos[(θ + φ)/2]cos[(θ - φ)/2]和cosθ - cosφ = -2sin[(θ + φ)/2]sin[(θ - φ)/2]。积化和差公式包括sinαcosβ = [sin(α + β) + sin(α - β)]/2、cosαsinβ = [sin(α + β) - sin(α - β)]/2、cosαcosβ = [cos(α + β) + cos(α - β)]/2和sinαsinβ = -[cos(α + β) - cos(α - β)]/2。

此外，还有一些常用的三角函数恒等式。同角三角函数关系包括sin²θ + cos²θ = 1、tan²θ + 1 = sec²θ和1 + cot²θ = csc²θ。诱导公式如前面所述，是求解不同象限内三角函数值的重要工具。倍角公式和半角公式也如前所述，可以大大简化计算过程。

总之，三角函数公式是数学中的重要内容之一，掌握这些公式对于学习和应用相关领域知识具有重要意义。在学习三角函数公式时，需要注意公式的适用条件和符号变化，以及不同公式之间的联系和转化。通过不断练习和应用，可以加深对三角函数公式的理解和掌握程度，提高解题能力和效率。